前回の「地衡風」は、等圧線が直線の場合の風でした。
しかし現実には、等圧線は円形に曲がっていることがほとんどです。このとき、地衡風の2つの力(気圧傾度力・コリオリ力)に加えて、「遠心力」が無視できなくなります。
1. 傾度風とは
傾度風とは、「気圧傾度力」、「コリオリ力」、そして「遠心力」の3つの力が釣り合った状態で吹く風のことです。
風が低気圧の周りを回るか、高気圧の周りを回るかで、力の釣り合い方が異なります。
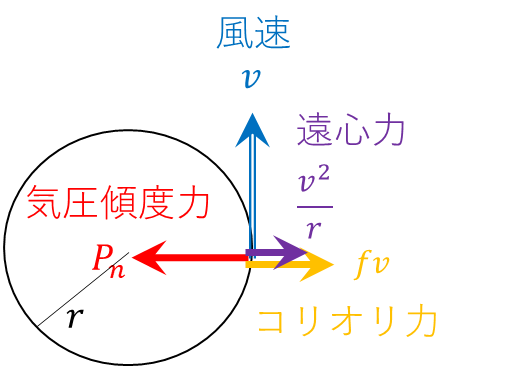
① 低気圧性循環(北半球では反時計回り)
低気圧の中心に向かおうとする「気圧傾度力」に対し、外側へ引っ張る「コリオリ力」と「遠心力」が対抗して釣り合います。
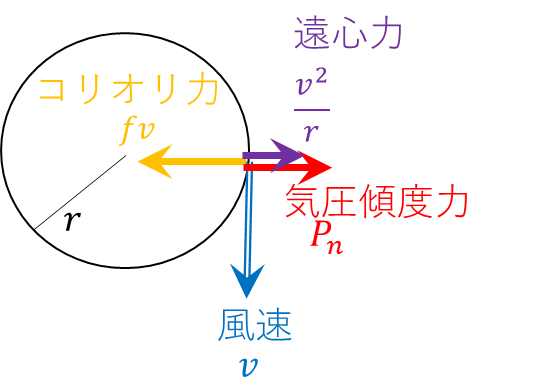
② 高気圧性循環(北半球では時計回り)
高気圧の中心から外へ押し出す「気圧傾度力」と、カーブの外へ飛び出そうとする「遠心力」の2つに対し、内側へ引き戻す「コリオリ力」が1つで対抗して釣り合います。
2. 傾度風の式
力の釣り合いを式で表すと以下のようになります。($P_n$:気圧傾度力、$f$:コリオリパラメータ、$v$:風速、$r$:半径)
低気圧の場合
$$P_n = fv + \frac{v^2}{r}$$
(気圧傾度力 = コリオリ力 + 遠心力)
高気圧の場合
$$fv = P_n + \frac{v^2}{r}$$
(コリオリ力 = 気圧傾度力 + 遠心力)
3. 地衡風との風速比較
ここが試験で最も問われるポイントです。
「もし、等圧線の間隔(気圧傾度力 $P_n$)がまったく同じだったら、風速はどうなるか?」
を比較します。
同じ気圧傾度力の下では、風速は以下の順になります。
高気圧性循環 > 地衡風 > 低気圧性循環
なぜこうなるのか、力の釣り合いから紐解きましょう。
地衡風と低気圧性循環の傾度風の比較
低気圧の釣り合いの式は $P_n = fv + \frac{v^2}{r}$ です。
気圧傾度力($P_n$)という「全体のエネルギー」を、コリオリ力と遠心力の2人で分担して支えています。
遠心力が手伝ってくれる分、コリオリ力($fv$)は小さくて済みます。
$f$ は定数なので、コリオリ力が小さいということは、風速 $v$ も小さく(遅く)なります。
地衡風と高気圧性循環の傾度風の比較
高気圧の釣り合いの式は $fv = P_n + \frac{v^2}{r}$ です。
コリオリ力($fv$)は、気圧傾度力($P_n$)だけでなく、遠心力($\frac{v^2}{r}$)まで一人で支えなければなりません。
大きな力が必要になるため、風速 $v$ は大きく(速く)ならざるを得ません。
4. 低気圧の中心付近での風速低下
もう一つ、重要な性質があります。
**「同じ気圧傾度であっても、低気圧の中心に近づく(回転半径 $r$ が小さくなる)ほど、風速は弱くなる」**という現象です。
低気圧の釣り合いの式をもう一度見てみましょう。
$$P_n = fv + \frac{v^2}{r}$$
中心に近づくと、カーブがきつくなり、半径 $r$ が非常に小さくなります。
すると、遠心力項($\frac{v^2}{r}$)が急激に大きくなります。
一定の気圧傾度力($P_n$)の中で、遠心力が大きな割合を占めるようになると、その分コリオリ力($fv$)に割り当てられる分が減ってしまいます。その結果、風速 $v$ を落とすことでバランスを取ろうとするのです。
🌪️ 台風の眼の壁
台風の中心付近で猛烈な風が吹くのは、中心付近の気圧傾度($P_n$)が桁違いに大きいからです。
もし、「台風の外側」と「台風の眼のすぐそば」で等圧線の間隔が同じだったとしたら、眼のそばの方が風は弱くなります(遠心ブレーキがかかるため)。
まとめ
- 低気圧性循環(反時計回り): 気圧傾度力 = コリオリ力 + 遠心力
- 高気圧性循環(時計回り): コリオリ力 = 気圧傾度力 + 遠心力
- 風速の大小関係(気圧傾度が同じ時): 高気圧性循環 > 直線(地衡風) > 低気圧性循環

