気象現象の根本的なエネルギー源は太陽です。
この単元「大気の放射」は、学科試験(一般知識)の最頻出分野の一つであり、実技試験の基礎ともなる非常に重要なパートです。計算問題としても出題されやすいため、法則の名前と公式、そして定性的な意味(「温度が上がるとどうなるか?」など)をしっかり押さえましょう。
1. 地球の公転と南中高度
地球は太陽の周りを1年かけて公転しています。この時、地軸(自転軸)が公転面の垂直方向に対して23.4度傾いていることが、季節変化を生み出します。
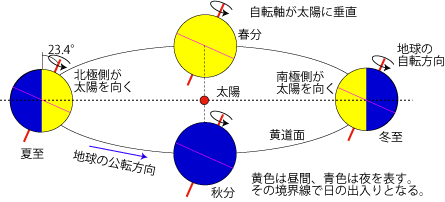
引用元:国立天文台HP
南中高度の計算式
ある地点(緯度 $\phi$)における、太陽が真南に来た時の高度(南中高度 $h$)は以下の式で表されます。
- $\phi$ (ファイ):観測地点の緯度
- $\delta$ (デルタ):太陽の赤緯(太陽が真上に来る緯度)
💡 試験対策のポイント
赤緯 $\delta$ の値は季節によって決まっています。暗記必須です。
- 夏至のとき:$\delta = +23.4^\circ$
- 冬至のとき:$\delta = -23.4^\circ$
- 春分・秋分のとき:$\delta = 0^\circ$
例:北緯35度の地点の夏至の南中高度は、$90 – 35 + 23.4 = 78.4^\circ$ となります。
2. 太陽定数
太陽定数とは、地球の大気上端において、太陽光線に垂直な面が受ける単位面積・単位時間あたりのエネルギー量のことです。
- 値: 約 $1.37 \, \text{kW/m}^2$ ($1366 \, \text{W/m}^2$)
「定数」と呼ばれますが、実際には地球と太陽の距離の変化(近日点・遠日点)や、太陽活動(黒点数など)によってわずかに変動します。
3. 太陽高度と放射強度の変化
地表面が受け取るエネルギー量は、太陽高度(地面に対する太陽の角度)によって大きく変化します。
入射角度による変化
太陽高度を $h$、太陽光線に垂直な面の強度を $I_0$ とすると、水平面が受ける放射強度 $I$ は以下のようになります。
- 高度が高い(昼間・夏): $\sin h$ が大きくなり、エネルギーが狭い範囲に集中するため、強度が大きくなる。
- 高度が低い(朝夕・冬): $\sin h$ が小さくなり、エネルギーが広い範囲に分散するため、強度が小さくなる。
また、高度が低いと大気中を通過する距離(光学的厚さ)が長くなるため、散乱や吸収を受けやすく、地上に届くエネルギーはさらに減少します。
4. アルベド(反射率)
アルベドとは、入射した放射エネルギーに対する、反射されたエネルギーの比率のことです。
- 地球全体の平均アルベド: 約 0.3(30%)
※太陽からのエネルギーの3割は宇宙へそのまま反射され、残り7割が地球(大気と地表)に吸収されます。 - 物質による違い:
- 新雪:0.8 ~ 0.9(非常に高い)
- 雲:0.3 ~ 0.8(厚さによる)
- 海面・森林:0.1 以下(低い=よく吸収する)
5. ステファン・ボルツマンの法則
あらゆる物体は、その温度に応じたエネルギーを放射しています(黒体放射)。
「物体の温度が高いほど、放出される全エネルギー量は急激に増える」という法則です。
公式
単位面積、単位時間あたりに黒体から放出される全エネルギー $I$ は、絶対温度 $T$ の4乗に比例します。
$$I = \sigma T^4$$
$\sigma$(シグマ):ステファン・ボルツマン定数
$\sigma = 5.67 \times 10^{-8} \, \text{W}/(\text{m}^2 \cdot \text{K}^4)$
💡 試験対策のポイント
「温度が2倍になると、放射エネルギーは何倍になるか?」という問題が頻出です。
$2^4 = 16$ なので、答えは16倍になります。
6. プランクの法則
ステファン・ボルツマンの法則が「全エネルギー量」を示すのに対し、プランクの法則は「どの波長にどれくらいの強さのエネルギーがあるか(スペクトル分布)」を示します。
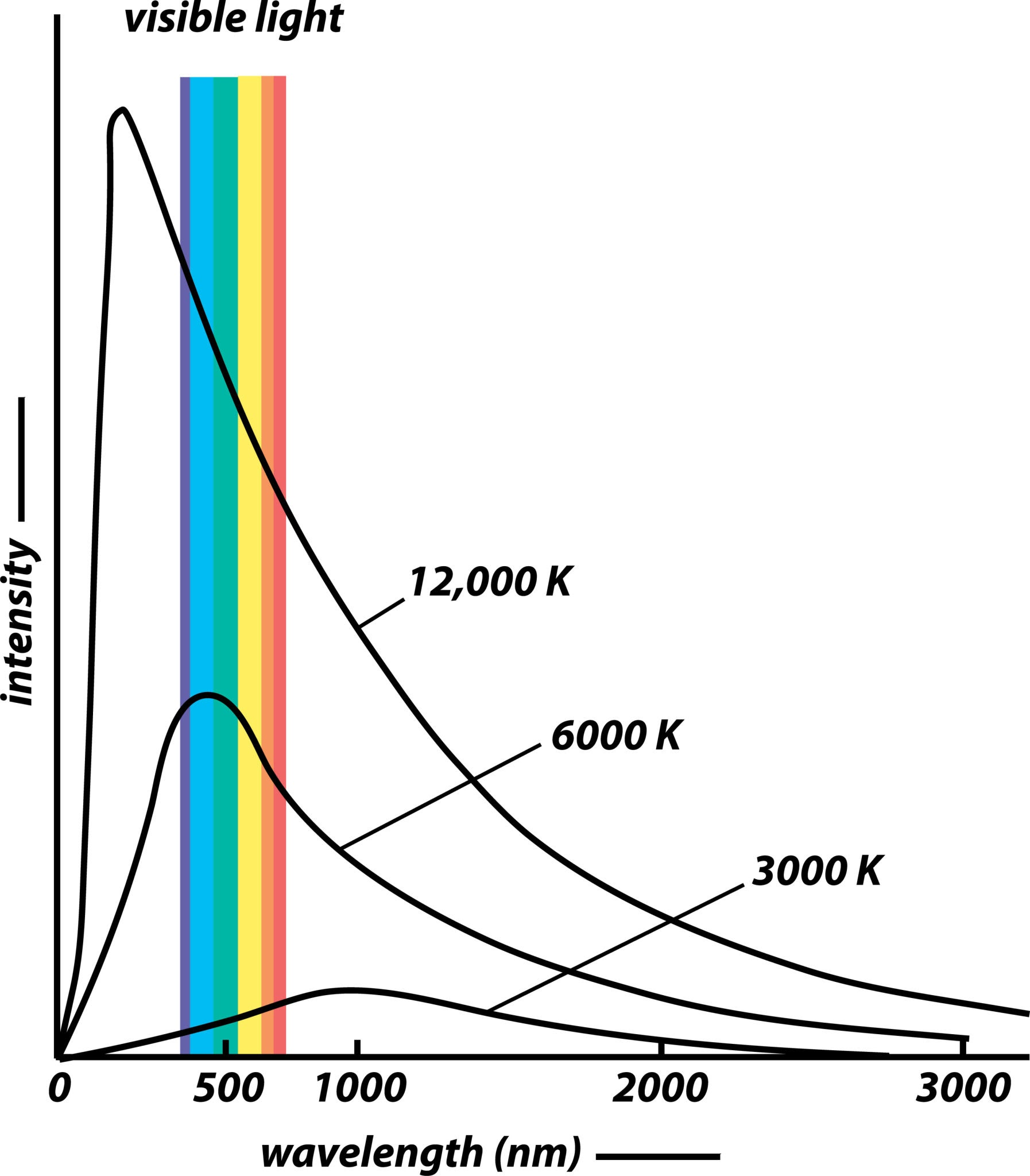
- 温度が高い物体ほど、あらゆる波長で放射強度が強くなります(グラフ全体が上に持ち上がる)。
- 温度によって、放射のピークとなる波長が異なります(後述のウィーンの変位則)。
7. ウィーンの変位則
プランクの法則のグラフにおいて、放射強度が最大となる波長(ピーク波長)は、温度に反比例するという法則です。
公式
ピーク波長 $\lambda_{max}$ と絶対温度 $T$ の関係:
この法則により、太陽放射と地球放射の違いが説明できます。
| 表面温度 ($T$) | ピーク波長 ($\lambda_{max}$) | 放射の種類 | |
|---|---|---|---|
| 太陽 | 約 $6000 \, \text{K}$ | 約 $0.5 \, \mu\text{m}$ | 短波放射 (可視光線が中心) |
| 地球 | 約 $300 \, \text{K}$ | 約 $10 \, \mu\text{m}$ | 長波放射 (赤外線が中心) |
8. キルヒホッフの法則
ある波長において、物体が放射を吸収する能力と、放出する能力の関係を示した法則です。
「ある波長の放射をよく吸収する物体は、その波長の放射をよく放出する」(良き吸収体は、良き放射体である)と言い換えられます。
- $\epsilon_\lambda$:その波長における射出率(出しやすさ)
- $\alpha_\lambda$:その波長における吸収率(吸いやすさ)
🌍 気象学での重要性
大気中の温室効果ガス(水蒸気や二酸化炭素など)は、「可視光線(太陽放射)は通すが、赤外線(地球放射)はよく吸収し、よく放出する」という選択的な性質を持っています。これが温室効果のメカニズム理解に繋がります。

