これまで学んだ「地衡風」や「傾度風」は、地球規模や天気図スケール(数百km〜数千km)の風でした。そこでは、地球の自転による「コリオリ力」が主役の一つでした。
しかし、竜巻のように、ごく狭い範囲でグルグルと回転する風の場合、話が変わってきます。
コリオリ力を無視して、「気圧傾度力」と「遠心力」の2つだけで釣り合う風、それが旋衡風(せんこうふう)です。
1. 旋衡風とは
旋衡風とは、回転半径が非常に小さいため、コリオリ力よりも「遠心力」が圧倒的に大きくなり、気圧傾度力と釣り合っている風のことです。
力の釣り合い
中心に向かって引っ張る「気圧傾度力」と、回転の外へ飛び出そうとする「遠心力」が釣り合っています。
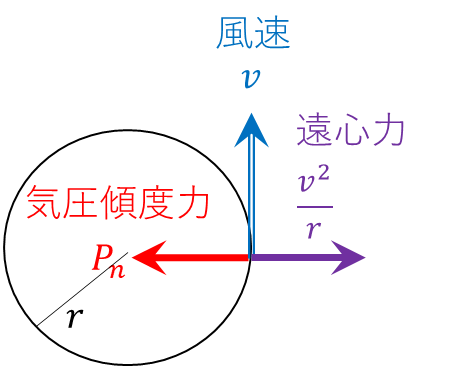
※ コリオリ力は小さすぎるため無視!
旋衡風の式
力の釣り合い式は非常にシンプルです。
$$
\frac{v^2}{r} = \frac{1}{\rho} \frac{\Delta P}{\Delta n}
$$
- $\frac{v^2}{r}$:遠心力($v$:風速, $r$:半径)
- $\frac{1}{\rho} \frac{\Delta P}{\Delta n}$:気圧傾度力
ここから風速 $v$ を求めると:
$$
v = \sqrt{\frac{r}{\rho} \frac{\Delta P}{\Delta n}}
$$
重要な特徴:回転方向は「どっちでもいい」
地衡風や傾度風は、北半球なら「低気圧は反時計回り」と決まっていました(コリオリ力のせい)。
しかし、旋衡風はコリオリ力を無視するため、理論上は時計回りでも反時計回りでも成立します。
- 気圧傾度力(内向き)と遠心力(外向き)さえ釣り合えば、どっちに回っていても力学的にOKなのです。
- ※ただし、現実の竜巻は親雲(メソサイクロン)の影響を受けるため、北半球では反時計回りが圧倒的に多いです。
2. 竜巻
旋衡風の代表例が竜巻です。
竜巻は、積乱雲の下に垂れ下がる漏斗雲を伴う、激しい空気の渦巻きです。
なぜあんなに風が強いのか?
旋衡風の式 $v = \sqrt{r \cdot P_n}$ を見ると、一見、半径 $r$ が小さい竜巻は風が弱そうに見えます。
しかし、竜巻の中心付近は気圧が極端に低いため、気圧傾度力 ($P_n$) が桁外れに大きいのです。
- 中心と外側の気圧差が猛烈に大きい(数kmの距離で100hPa違うことも)。
- 強烈な気圧傾度力が中心へ空気を引っ張る。
- それに対抗するために、猛烈な回転による遠心力が必要になる。
- 結果として、台風を超える大きな風速になる。
スケール
- 水平規模: 数十m 〜 数百m(極めて小さい)
- 寿命: 数分 〜 数十分(短い)
- 回転バランス: 遠心力が支配的(コリオリ力は無視)
💡 試験対策のまとめ
- 地衡風: 気圧傾度力 = コリオリ力 (直線・大規模)
- 傾度風: 気圧傾度力、コリオリ力、遠心力の3つ (曲線・低/高気圧)
- 旋衡風: 気圧傾度力 = 遠心力 (小規模・竜巻)

