天気図を見ると、風は等圧線に沿って吹いていることが多いことに気づきます。
「気圧傾度力は低気圧の方へ向かう力なのに、なぜ風は吸い込まれずに横(等圧線平行)に吹くのか?」
その答えが、気象学の理想的な風のモデルである地衡風(ちこうふう)です。
上空の摩擦のない世界(自由大気)では、この地衡風が実際の風の良い近似となります。
1. 地衡風とは
地衡風とは、「気圧傾度力」と「コリオリ力」の2つの力が釣り合った状態で吹く風のことです。
風が吹く仕組み(北半球)
- まず、気圧差によって「気圧傾度力」が生じ、空気は低気圧の方へ動き出します。
- 動き出すと(風速がつくと)、「コリオリ力」が進行方向の右側に働き始めます。
- 風速が増すにつれてコリオリ力も強くなり、風向きはどんどん右へ曲がっていきます。
- 最終的に、気圧傾度力(低気圧側)とコリオリ力(高気圧側)が一直線上で逆向きに釣り合います。
- このとき、風は等圧線に対して平行に吹き続けます。
力の釣り合い図(北半球)
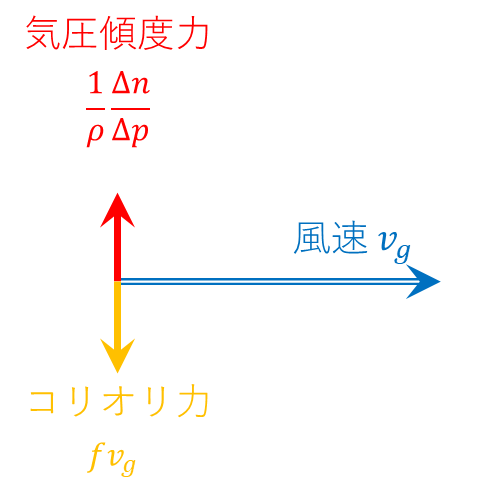
※北半球では、風の進行方向に対して「右側」にコリオリ力が働き、気圧傾度力と釣り合う。
💡 法則:バイス・バロットの法則
「北半球で風を背にして立つと、左手に低気圧、右手に高気圧がある」
これは地衡風の性質そのものを表しています。
2. 地衡風の式
地衡風の速度(風速)は、力の釣り合いの式から導くことができます。
$$
\text{気圧傾度力} = \text{コリオリ力}
$$
$$
\frac{1}{\rho} \frac{\Delta P}{\Delta n} = f v_g
$$
これを地衡風速 $v_g$ について解くと、以下の重要な式になります。
$$
v_g = \frac{1}{\rho f} \frac{\Delta P}{\Delta n}
$$
- $v_g$:地衡風の風速
- $\rho$:空気密度
- $f$:コリオリパラメータ ($2\Omega \sin \phi$)
- $\frac{\Delta P}{\Delta n}$:気圧傾度(気圧の変化率)
3. 気圧傾度や緯度との関係
試験では、上記の式を変形させずとも、「何がどうなると風が強くなるのか?」という関係性を直感的に理解しておくことが重要です。
① 気圧傾度との関係(比例)
式の分子に $\Delta P$ があることから分かります。
- 等圧線の間隔が狭い(気圧傾度が大きい)ほど、地衡風は強くなる。
- これは天気図を見たときの直感通りですね。
② 緯度との関係(反比例)
式を見ると、分母に $f$(コリオリパラメータ)があります。$f$ は緯度 $\phi$ が高いほど大きな値になります。
$$
v_g \propto \frac{1}{\sin \phi}
$$
つまり、「等圧線の間隔(気圧傾度)が同じならば」:
- 低緯度(赤道に近い)ほど、地衡風は強くなる。
- 高緯度(極に近い)ほど、地衡風は弱くなる。
🤔 なぜ?(イメージでの理解)
コリオリ力は「風速に比例して」強くなる力でした。
高緯度では地球の回転の影響($f$)が強いため、「遅い風速」でもすぐに十分なコリオリ力が生まれて、気圧傾度力と釣り合ってしまいます。
一方、低緯度では $f$ が弱いため、「速い風速」にならないと、気圧傾度力に対抗できるだけのコリオリ力が生まれないのです。
③ 密度との関係(反比例)
分母に $\rho$ があります。
- 密度が小さい(上空)ほど、地衡風は強くなる。
- 同じ気圧差なら、空気が軽い(スカスカな)方が、抵抗なく加速しやすいイメージです。
まとめ
| 項目 | 地衡風速への影響 | 理由 |
|---|---|---|
| 等圧線の間隔 | 狭いほど 強い | 押す力(気圧傾度力)が強いから |
| 緯度 | 低いほど 強い | コリオリ係数 $f$ が分母にあるから |
| 高度(密度) | 高いほど 強い | 密度 $\rho$ が分母にあるから |
地衡風は、あくまで「直線的」な等圧線でのモデルです。
次は、低気圧や高気圧のように「カーブしている」場所で吹く風、「傾度風(けいどふう)」について学びましょう。

